Podstawowe pojęcia¶
- $\text{Factorin}(x, T)$ - słowo $x$ występuje w tekście $T$
- $O(|x|)$ - oczekiwana złożoność operacji $\text{Factorin}$
- rozgałęzienie - elementarna operacja, stanowiąca punkt odniesienia złożoności
- $O\left(log(|\Sigma|)\right)$ - złożność obliczeniowa operacji rozgałęziania (dla znanego alfabetu można przyjąć jako stałą)
- algorytmy wyszukiwania wzorca w najlepszym przypadku wyliczają $\text{Factorin}$ w czasie $O(|T|)$
"Dobra" reprezentacja tekstu¶
- $x$ - wzorzec
- $T$ - tekst
$D$ - struktura danych reprezentująca tekst dla operacji $\text{Factorin}$
- $D$ - liniowa ze względu na długość tekstu (choć zbiór wszystkich pod-słów ma rozmiar $O(|T|^2)$)
- $D$ - konstruowana w czasie $O(|T|)$
- $D$ - pozwala wyliczyć $\text{Factorin}$ w czasie $O(|x|)$
Dobre reprezentacje tekstu¶
- drzewa sufiksów
- drzewa podsłów
Prawie dobre reprezentacje:
- tablice sufiksów
Drzewo trie "traj"¶
- sprawdzanie czy słowo jest w drzewie
- znajdowanie najdłuższego prefiksu słowa, który jest w drzewie
- wyszukiwanie wszystkich słów o zadanym prefiksie
Trie sufiksów¶
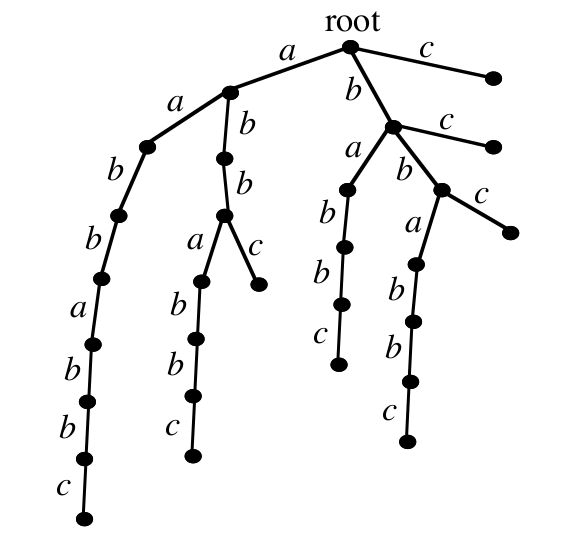
Własności trie sufiksów¶
- dowolna ścieżka od korzenia do dowolnego węzła jest pod-słowem
- ścieżki kończące się na liściu są sufiksami
- przyjmuje się, że ostatnia litera słowa występuje tylko raz (można dodać sztuczną literę do alfabetu)
Algorytm budowy trie sufiksów (szkic)¶
Oznaczenia:
- $T^{i}$ - sufiks tekstu $T$ o indeksie $i$, który ma być dodany do drzewa
- $D$ - trie sufiksów
- $head(T^{i}, D)$ - najdłuższy prefiks $T^{i}$ znajdujący się w $D$
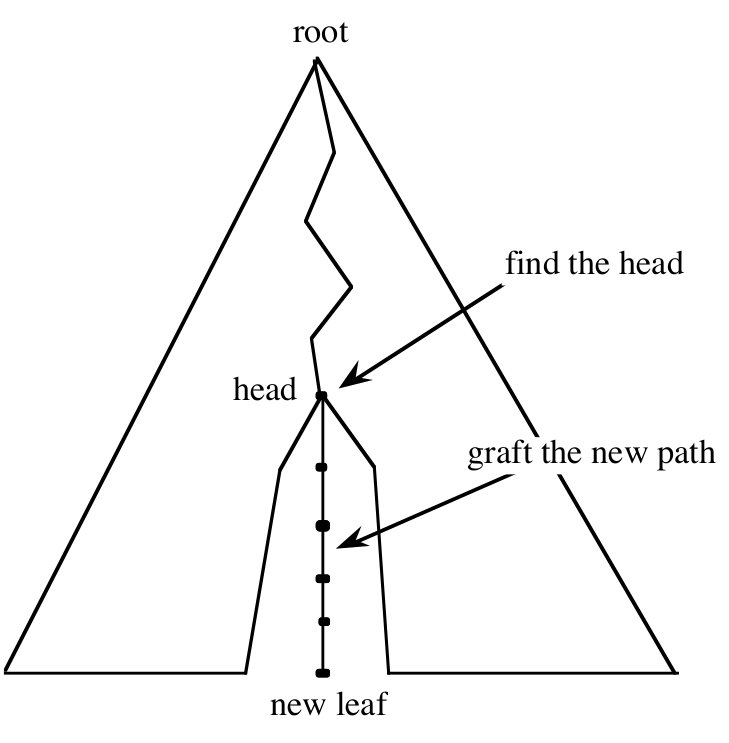
Algorytm:
- znajdź $head(T^{i}, D)$
- dodaj nową gałąź, rozpoczynającą się w węźle odpowiadającym $head(T^{i}, D)$
In [ ]:
def build_trie_schema(text):
trie = compute_initial_trie(text)
leaf = trie.leafs()[0]
for i in range(1, len(text)):
suffix = text[i:]
head = trie.find(suffix, leaf)
suffix_end = suffix[head.depth():]
leaf = head.graft(suffix_end)
return trie
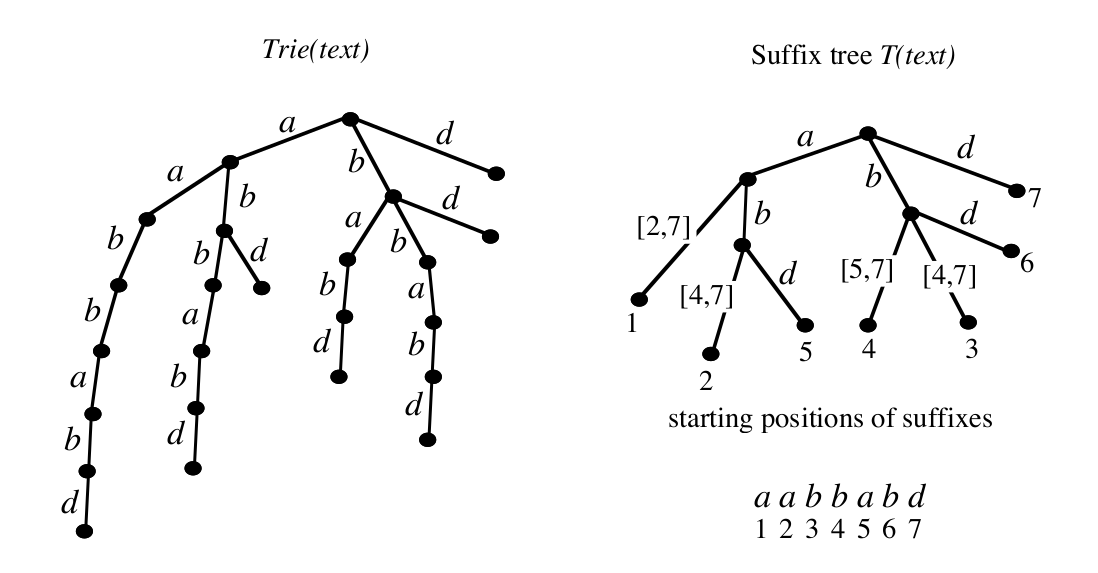
Alternatywny algorytm budowy trie¶
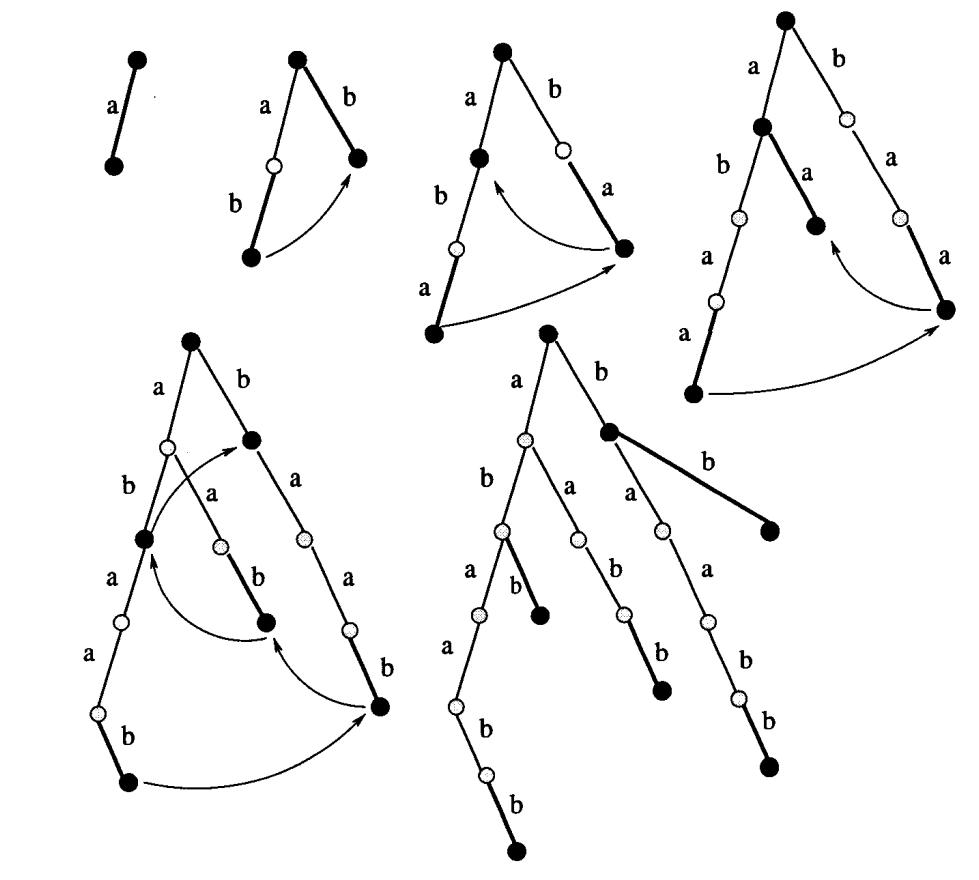
In [ ]:
tree = Tree()
# create first tree with root and one child
for i in range(1, len(text)):
a = text[i]
deepest # deepest leaf of tree
node = deepest.suffix_link
while((node != root) and (a not in node.children)):
child = node.add_child(a)
# add suffix links for the child
Dodawanie łączników¶
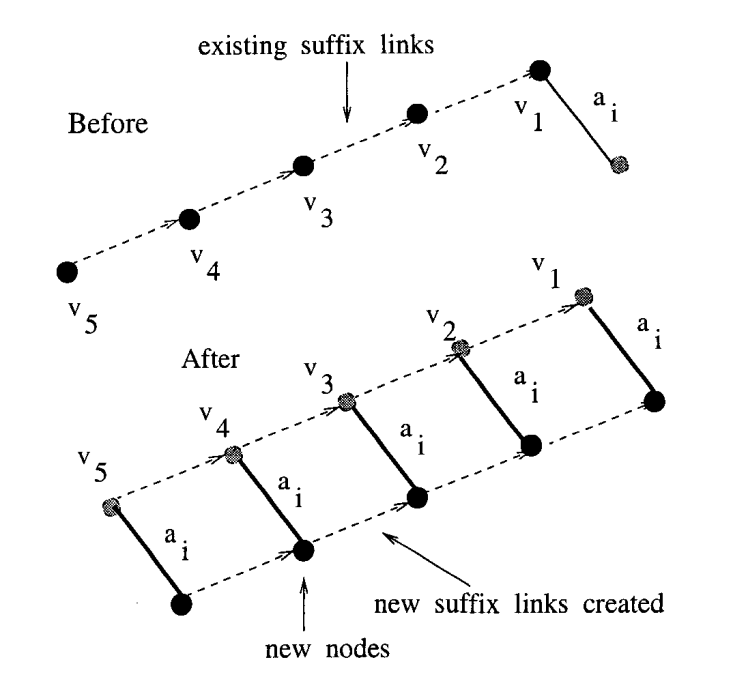
Węzły domniemane¶
- $(n, \alpha)$ - domniemany węzeł w drzewie $D$
- $n$ jest węzłem w drzewie $D$
- $\alpha$ jest właściwym prefiksem etykiety krawędzi prowadzącej do jednego dziecka węzła $n$
- $(n, \epsilon)$ - właściwy węzeł w drzewie $D$ = $n$
Węzły domniemane¶
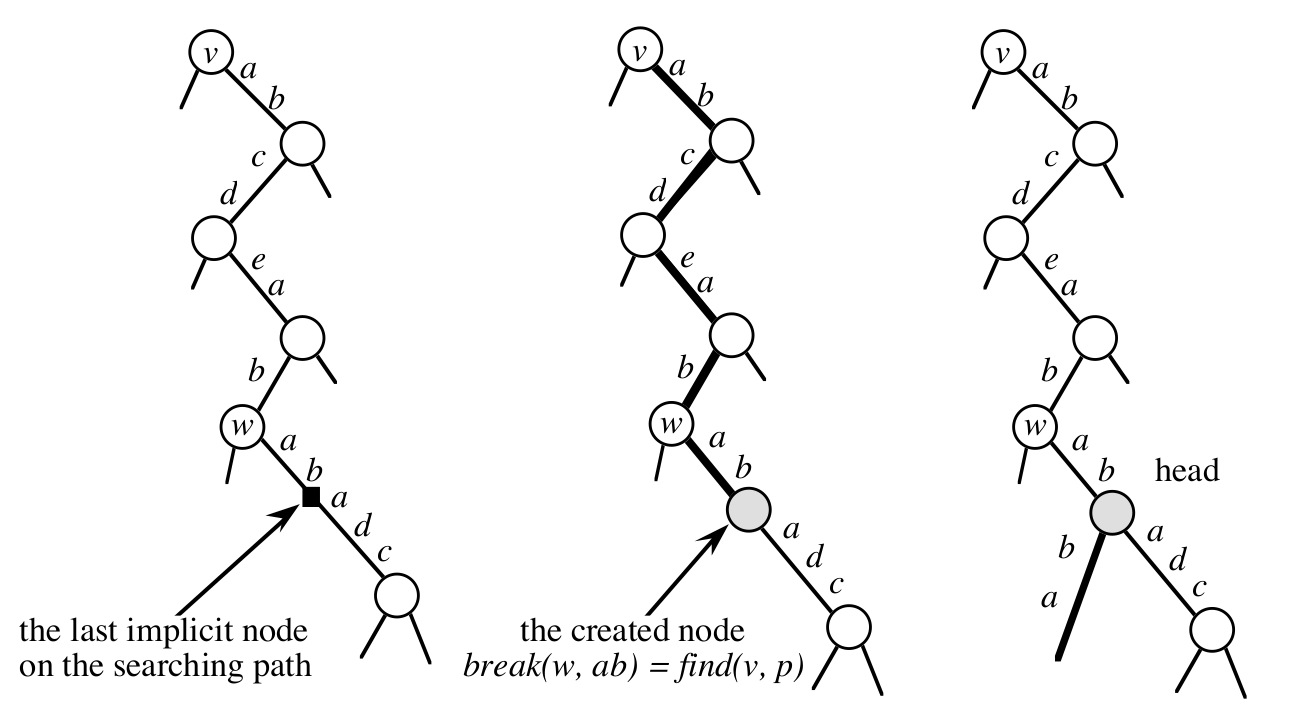
Domniemany łącznik¶
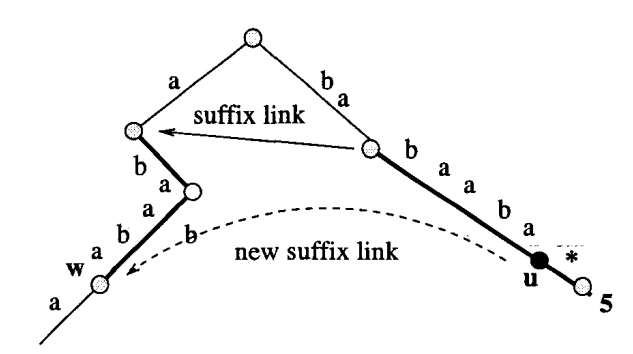
Algorytm Ukkonena¶
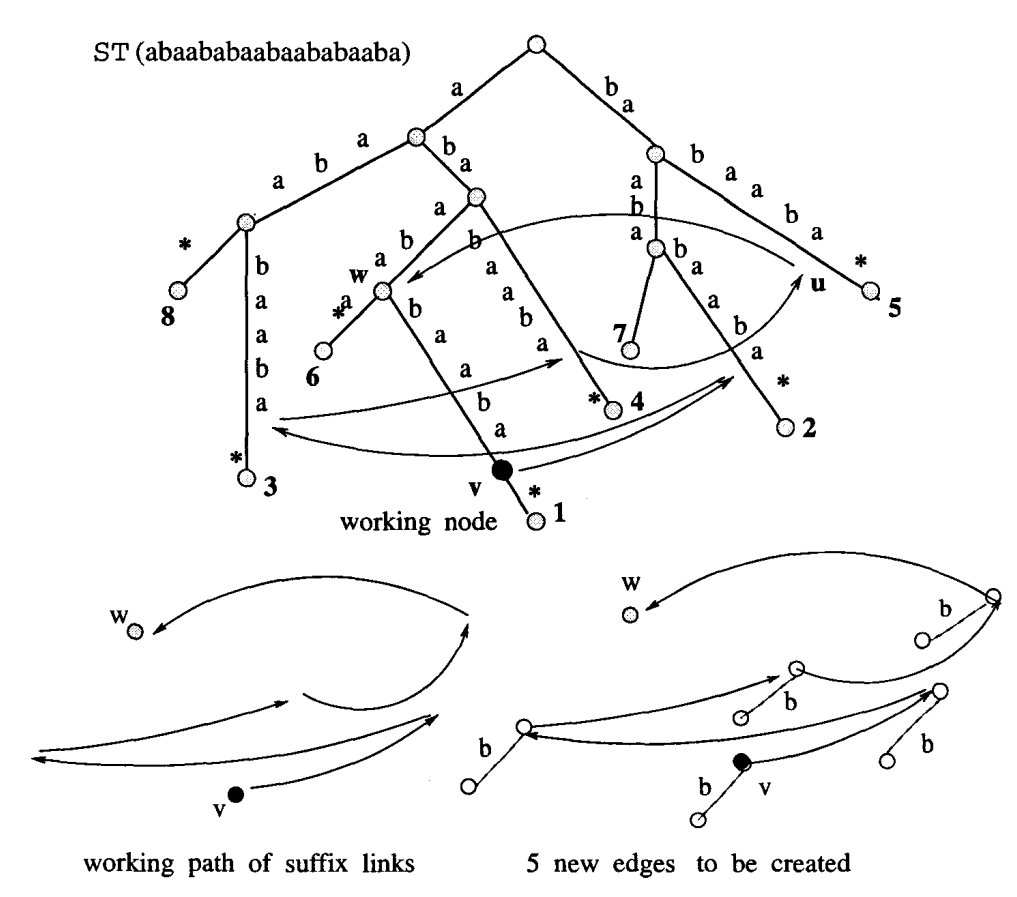
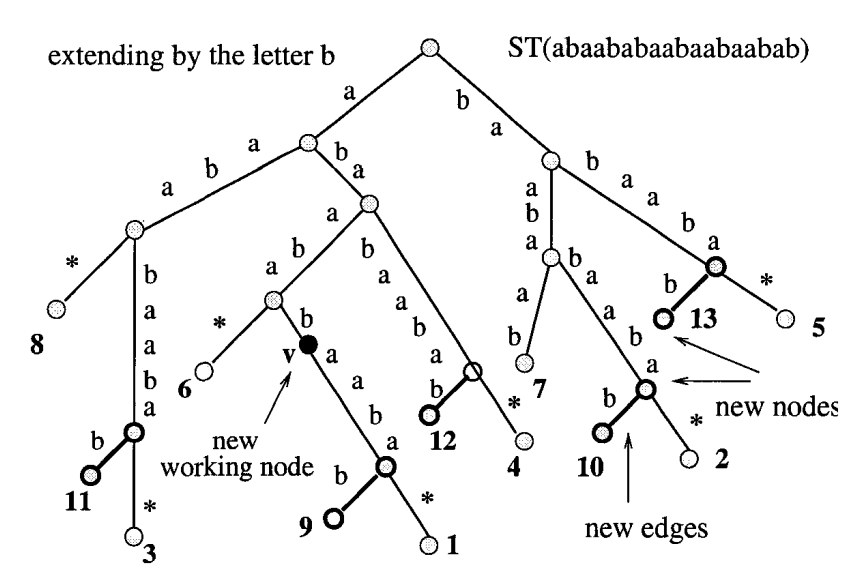
Algorytm Ukkonena¶
In [ ]:
tree = Tree()
# create first tree with root and one child
node = tree.root
for i in range(1, len(text)):
a = text[i]
if(a in node.children):
node = node.children[a]
# it's possible that the child has to be created
else:
node = node.implicit_suffix_link()
while((node != root) and (a not in node.children)):
child = node.add_child(a)
# add suffix links for the child
node = node.children[a]
Lemat 2.1 (rozmiar drzewa sufiksów)¶
Rozmiar drzewa sufiksów jest rzędu $O(|T|)$
Algorytm McCreighta¶
- kompresja trie na drzewo sufiksów nie jest optymalna ponieważ:
- rozmiar trie jest $O(|T|^2)$
- czas utworzenie trie jest $O(|T|^2)$
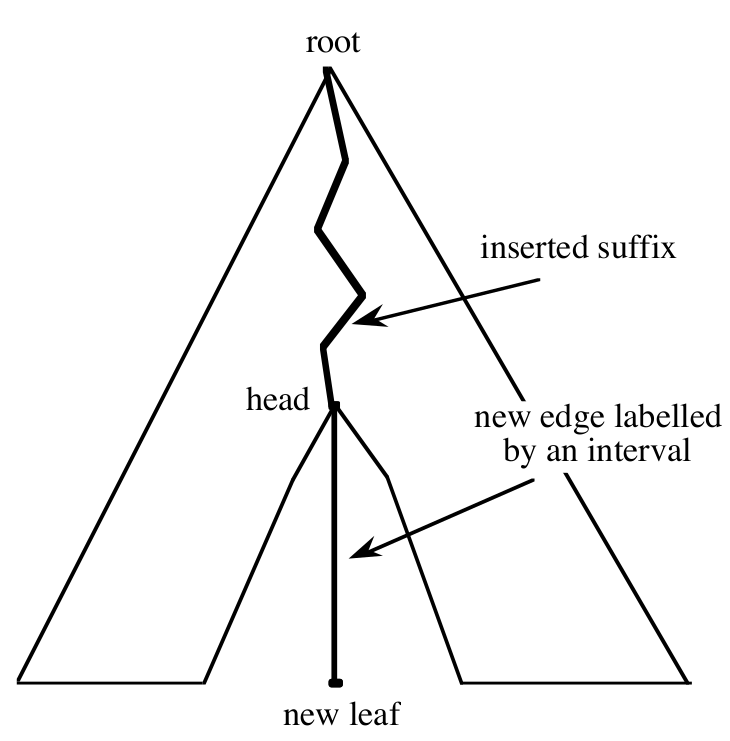
up-link-down¶
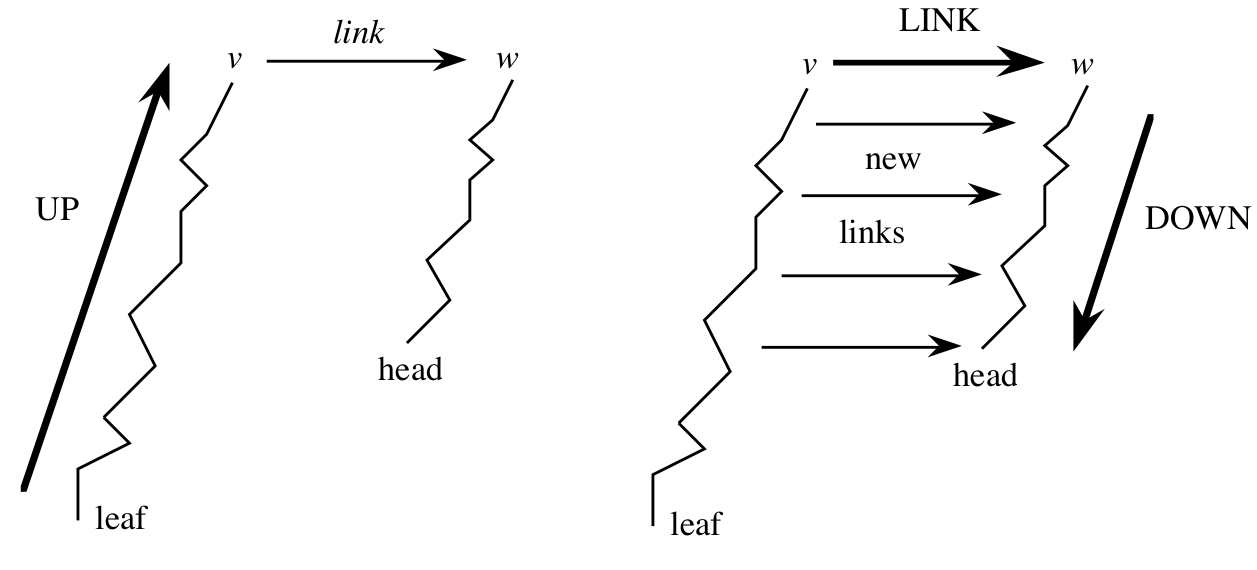
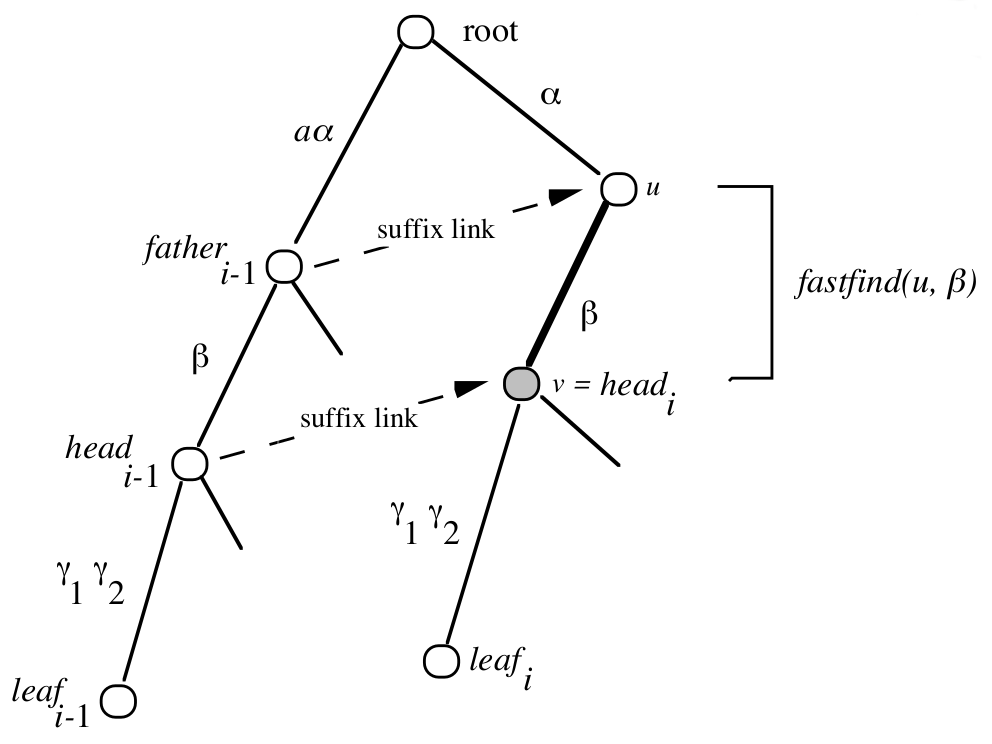
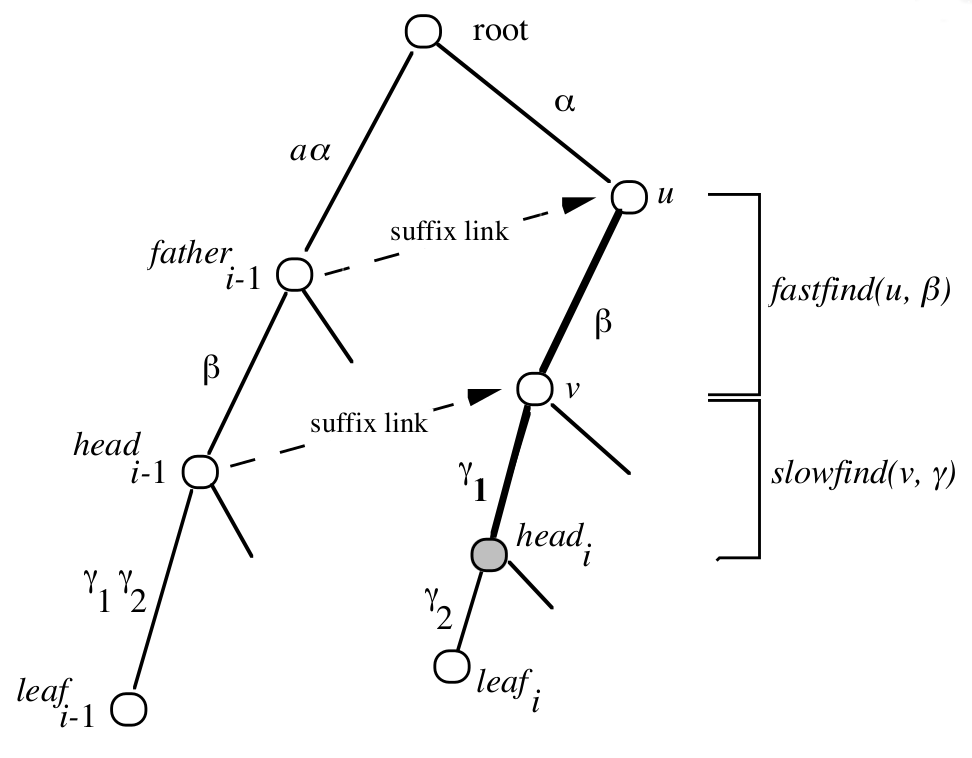
Algorytm McCreighta¶
In [ ]:
last_head = head = self.root
node = self.root
leaf = self.root.child(0)
text_length = len(text)
for i in range(1, text_length):
suffix = text[i:]
leaf_label = leaf.label()
head_label = head.label()
node = head.parent.link
node = node.fast_find(head_label)
if(node.size() == 1):
head = node
else:
head = node.slow_find(leaf_label)
leaf = head.graft(?)
last_head.add_link(node)
last_head = head